Advanced Course: Statistical Mechanics, Machine Learning, and Quantum Computing

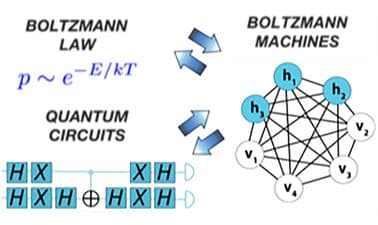
Course Description

This advanced-level course is a unique and innovative exploration that bridges three distinct fields: statistical mechanics, machine learning, and quantum computing. At its core, the course revolves around the unifying concept of a state-space with 2^N dimensions defined by N binary bits. This interdisciplinary approach provides students with a comprehensive understanding of how fundamental principles in physics can be applied to cutting-edge technologies and computational methods.

What Students Will Learn

• Boltzmann Law and its applications in statistical mechanics
• Principles and implementation of Boltzmann Machines in machine learning
• Transition Matrix theory and its relevance to computational methods
• Quantum Boltzmann Law and its implications for quantum systems
• Quantum Gates and their role in quantum computing algorithms

Prerequisites

This course is designed for students with a strong background in engineering or physical sciences. Participants should have a solid foundation in:

• Differential equations
• Linear algebra
• Basic concepts in physics and mechanics

Course Coverage

• Fundamentals of statistical mechanics, including entropy and free energy
• Boltzmann Machines and their applications in machine learning
• Markov Chain Monte Carlo methods and Gibbs Sampling
• Quantum spin systems and quantum annealing
• Quantum computing concepts, including Grover's search algorithm and Shor's algorithm
• The transition from classical to quantum computational models

Target Audience

• Advanced undergraduate or graduate students in engineering, physics, or computer science
• Professionals working in fields related to machine learning or quantum computing
• Researchers interested in interdisciplinary applications of statistical mechanics
• Anyone with a strong mathematical background looking to expand their knowledge in cutting-edge computational methods

Real-World Applications

• Developing more efficient machine learning algorithms for complex problem-solving
• Designing and optimizing quantum computing systems
• Advancing research in fields such as materials science, cryptography, and drug discovery
• Improving optimization techniques for large-scale industrial processes
• Enhancing data analysis methods in fields like finance, healthcare, and climate science

Syllabus

Epilogue

This course offers a unique opportunity to delve into the fascinating intersections of statistical mechanics, machine learning, and quantum computing. By mastering these concepts, students will be well-equipped to tackle some of the most challenging problems in modern science and technology, positioning themselves at the forefront of innovation in their respective fields.